통계
1. 통계의 정의와 목적
- 데이터를 통해 특정 현상의 패턴을 이해하고, 이를 기반으로 예측하거나 의사 결정을 지원하는 데 활용
- 기술통계(Descriptive Statistics)와 추론통계(Inferential Statistics)로 구분
1) 기술통계(Descriptive Statistics)
- 기술통계는 데이터를 요약하고 정리하여 쉽고 빠르게 주요 특징을 이해할 수 있도록 표현하는 방법을 다룬다.
(1) 중심 경향 측정 (Central Tendency)
- 중심 경향 측정은 데이터의 중심 값을 찾는 방법
- 평균(Mean): 데이터 값들의 총합을 데이터 개수로 나눈 값. 데이터가 정규분포를 따를 때 대표적인 값이 된다.
- 장점: 전체적인 흐름을 쉽게 파악 가능
- 단점: 이상치(outlier)에 민감하여 왜곡될 가능성이 있음
- 중앙값(Median): 데이터를 크기순으로 정렬했을 때, 중앙에 위치하는 값.
- 장점: 이상치의 영향을 받지 않음
- 단점: 데이터의 전체적인 특성을 나타내기에 부족할 수 있음
- 최빈값(Mode): 데이터에서 가장 자주 등장하는 값.
- 장점: 범주형 데이터에서 유용하게 사용됨
- 단점: 데이터에 따라 최빈값이 없거나, 여러 개가 존재할 수 있음
- 평균(Mean): 데이터 값들의 총합을 데이터 개수로 나눈 값. 데이터가 정규분포를 따를 때 대표적인 값이 된다.
(2) 산포도 측정 (Dispersion)
- 산포도는데이터가 평균을 중심으로 얼마나 퍼져 있는지를 분석하는 것이 중요.
- 범위(Range): 데이터의 최댓값과 최솟값의 차이를 의미
- 분산(Variance): 데이터 값들이 평균에서 얼마나 떨어져 있는지를 나타내는 지표로 값이 클수록 데이터의 변동성이 크다는 것을 의미.
- 표준편차(Standard Deviation): 분산의 제곱근을 구한 값으로, 데이터가 평균에서 얼마나 떨어져 있는지를 쉽게 해석할 수 있도록 변환한 값. 값이 클수록 데이터가 퍼져 있고, 작을수록 데이터가 평균에 가까운 값으로 모여 있음을 의미.
- 사분위 범위(Interquartile Range, IQR): 데이터의 1사분위(Q1)와 3사분위(Q3) 사이의 범위를 의미하며, 이상치를 판별하는 데 유용
(3) 데이터 시각화
- 히스토그램(Histogram): 데이터의 분포를 막대 그래프로 표현
- 박스플롯(Box Plot): 사분위수와 이상치를 한눈에 볼 수 있도록 정리
- 산점도(Scatter Plot): 두 변수 간의 관계를 나타내는 그래프
2) 추론통계(Inferential Statistics)
- 표본 데이터를 이용하여 모집단(population)의 특성을 추정하는 방법. 일부 데이터를 분석하여 전체 데이터를 예측..
(1) 가설검정(Hypothesis Testing)
- 가설검정은 주어진 데이터가 특정 가설을 뒷받침하는지 여부를 판단하는 과정
- 귀무가설(Null Hypothesis, H₀): "차이가 없다"는 기본 가설
- 대립가설(Alternative Hypothesis, H₁): "차이가 있다"는 가설
- 유의수준(Significance Level, α): 일반적으로 5%(0.05)를 사용, p-value가 이 값보다 작으면 귀무가설을 기각
- ex. 예를 들어, 어떤 신약이 기존 치료제보다 효과가 있는지를 검정하려면:
- 귀무가설(H₀): "신약과 기존 치료제의 효과 차이가 없다."
- 대립가설(H₁): "신약이 기존 치료제보다 효과가 있다."
- 실험을 통해 얻은 p-value가 0.03이면 유의수준 0.05보다 작으므로 귀무가설을 기각하고, 신약이 효과가 있다고 판단할 수 있음.
(2) 신뢰구간(Confidence Interval)
- 신뢰구간은 모집단의 평균을 포함할 가능성이 높은 값의 범위를 제공하는 개념
- 예를 들어, 어떤 제품의 평균 수명이 50시간이고 표준편차가 5시간이며, 95% 신뢰구간을 구하면 특정 범위 내에서 평균값이 존재할 확률이 95%임을 의미.
(3) 회귀분석(Regression Analysis)
- 회귀분석은 변수 간의 관계를 수학적으로 모델링하는 방법입니다.
- 단순 선형 회귀(Simple Linear Regression)
- 하나의 독립변수가 종속변수에 미치는 영향을 분석하는 모델
- 공식: 여기서 X는 독립변수, Y는 종속변수, a는 기울기, b는 절편을 의미
- Y = aX + b
- 단순 선형 회귀(Simple Linear Regression)
- 다중 선형 회귀(Multiple Linear Regression)
- 여러 개의 독립변수가 종속변수에 영향을 미치는 모델
- 회귀분석 예시
- 예를 들어, 광고비(X)와 제품 판매량(Y) 간의 관계를 분석할 때:
- X가 증가할수록 Y도 증가하면, 긍정적인 관계(양의 상관관계)
- X가 증가할수록 Y가 감소하면, 부정적인 관계(음의 상관관계)
- 예를 들어, 광고비(X)와 제품 판매량(Y) 간의 관계를 분석할 때:
2. 통계 예제
1) A/B 테스트 (T-검정 활용)
- 이메일 마케팅 캠페인에서 제목을 다르게 설정하여 두 그룹(A/B)으로 테스트함.
- A 그룹(기존 제목)과 B 그룹(새로운 제목)에서 이메일을 연 클릭률(CTR)을 비교하여 어떤 제목이 더 효과적인지 확인.
import numpy as np
from scipy import stats
# A/B 테스트 데이터 (CTR %)
group_A = [12, 15, 14, 10, 16, 14, 13, 15] # 기존 제목
group_B = [18, 21, 19, 22, 20, 23, 21, 22] # 새로운 제목
# 독립표본 T-검정 수행
t_stat, p_value = stats.ttest_ind(group_A, group_B)
print(f"T-검정 통계량: {t_stat}")
print(f"P-값: {p_value}")
if p_value < 0.05:
print("귀무가설 기각: 새로운 제목(B)이 기존 제목(A)보다 유의미하게 CTR이 높음")
else:
print("귀무가설 채택: 두 제목 간 CTR 차이가 없음")


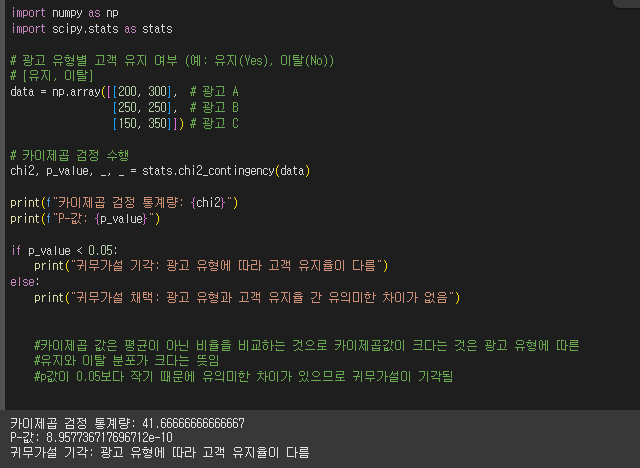
2) 고객 유지율 분석 (카이제곱 검정 활용)
- 신규 고객 중 30일 후에도 서비스를 사용하는 고객과 그렇지 않은 고객을 분석.
- 가입한 고객 중에서 지속 사용 여부가 광고 유형에 따라 차이가 있는지 검증.
import numpy as np
import scipy.stats as stats
# 광고 유형별 고객 유지 여부 (예: 유지(Yes), 이탈(No))
# [유지, 이탈]
data = np.array([[200, 300], # 광고 A
[250, 250], # 광고 B
[150, 350]]) # 광고 C
# 카이제곱 검정 수행
chi2, p_value, _, _ = stats.chi2_contingency(data)
print(f"카이제곱 검정 통계량: {chi2}")
print(f"P-값: {p_value}")
if p_value < 0.05:
print("귀무가설 기각: 광고 유형에 따라 고객 유지율이 다름")
else:
print("귀무가설 채택: 광고 유형과 고객 유지율 간 유의미한 차이가 없음")
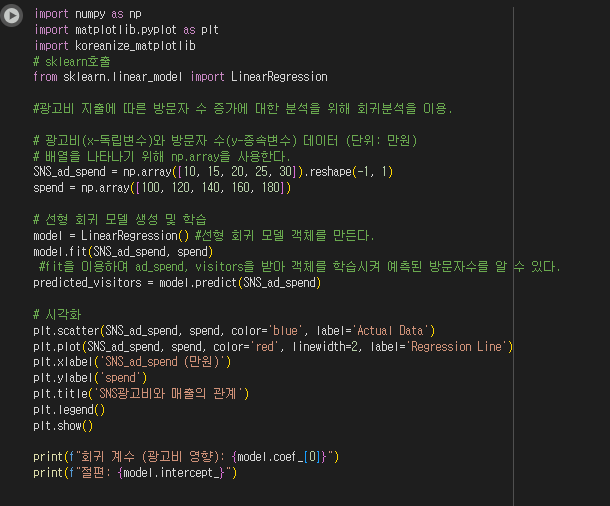
3) 광고 ROI 예측 (회귀 분석 활용)
- 광고비 지출에 따라 웹사이트 방문자 수가 증가하는 패턴을 분석.
- 선형 회귀 분석을 사용하여 광고비가 방문자 수에 미치는 영향을 예측.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 광고비(x)와 방문자 수(y) 데이터 (단위: 만원)
ad_spend = np.array([10, 20, 30, 40, 50, 60, 70, 80]).reshape(-1, 1)
visitors = np.array([100, 200, 280, 350, 400, 500, 620, 700])
# 선형 회귀 모델 생성 및 학습
model = LinearRegression()
model.fit(ad_spend, visitors)
# 예측 수행
predicted_visitors = model.predict(ad_spend)
# 시각화
plt.scatter(ad_spend, visitors, color='blue', label='Actual Data')
plt.plot(ad_spend, predicted_visitors, color='red', linewidth=2, label='Regression Line')
plt.xlabel('Ad Spend (만원)')
plt.ylabel('Visitors')
plt.title('광고비와 방문자 수의 관계')
plt.legend()
plt.show()
print(f"회귀 계수 (광고비 영향): {model.coef_[0]}")
print(f"절편: {model.intercept_}")
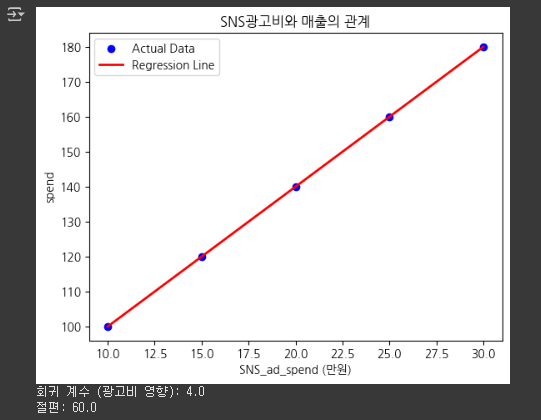
3-1) 광고비와 매출 관계 분석
- 한 회사는 광고비가 매출에 미치는 영향을 분석하고자 한다. 아래 데이터를 사용하여 다중회귀분석을 수행하라.
| SNS 광고비(만원) | 검색 광고비(만원) | 배너 광고비(만원) | 매출(만원) |
| 10 | 20 | 5 | 100 |
| 15 | 25 | 7 | 120 |
| 20 | 30 | 8 | 140 |
| 25 | 35 | 10 | 160 |
| 30 | 40 | 12 | 180 |
import numpy as np
from sklearn.linear_model import LinearRegression
# 광고 유형별 데이터 (단위: 만원)
sns_ad = np.array([10, 15, 20, 25, 30]).reshape(-1, 1)
search_ad = np.array([20, 25, 30, 35, 40]).reshape(-1, 1)
banner_ad = np.array([5, 7, 8, 10, 12]).reshape(-1, 1)
sales = np.array([100, 120, 140, 160, 180]) # 매출 (만원)
# 각 광고 유형별 단순 선형 회귀 모델 학습
models = {
"SNS 광고비": LinearRegression(),
"검색 광고비": LinearRegression(),
"배너 광고비": LinearRegression()
}
ads = {
"SNS 광고비": sns_ad,
"검색 광고비": search_ad,
"배너 광고비": banner_ad
}
# 모델 학습
coefficients = {}
intercepts = {}
for ad_type, model in models.items():
model.fit(ads[ad_type], sales) # 학습
coefficients[ad_type] = model.coef_[0]
intercepts[ad_type] = model.intercept_
# 광고비 설정 (여기에서 원하는 광고비를 변경할 수 있음)
sns_budget = 40 # SNS 광고비 (만원)
search_budget = 50 # 검색 광고비 (만원)
banner_budget = 13 # 배너 광고비 (만원)
# 매출 예측
sns_sales = coefficients["SNS 광고비"] * sns_budget + intercepts["SNS 광고비"]
search_sales = coefficients["검색 광고비"] * search_budget + intercepts["검색 광고비"]
banner_sales = coefficients["배너 광고비"] * banner_budget + intercepts["배너 광고비"]
# 최종 매출 평균값으로 계산
predicted_sales = (sns_sales + search_sales + banner_sales) / 3
# 예측 결과 출력
print(f"광고비 설정: SNS={sns_budget}만원, 검색={search_budget}만원, 배너={banner_budget}만원")
print(f"예상 평균 매출액: {predicted_sales:.2f} 만원")
print(f"SNS 광고비 : {sns_sales}")
print(f"검색 광고비 : {search_sales}")
print(f"배너 광고비 : {banner_sales}")

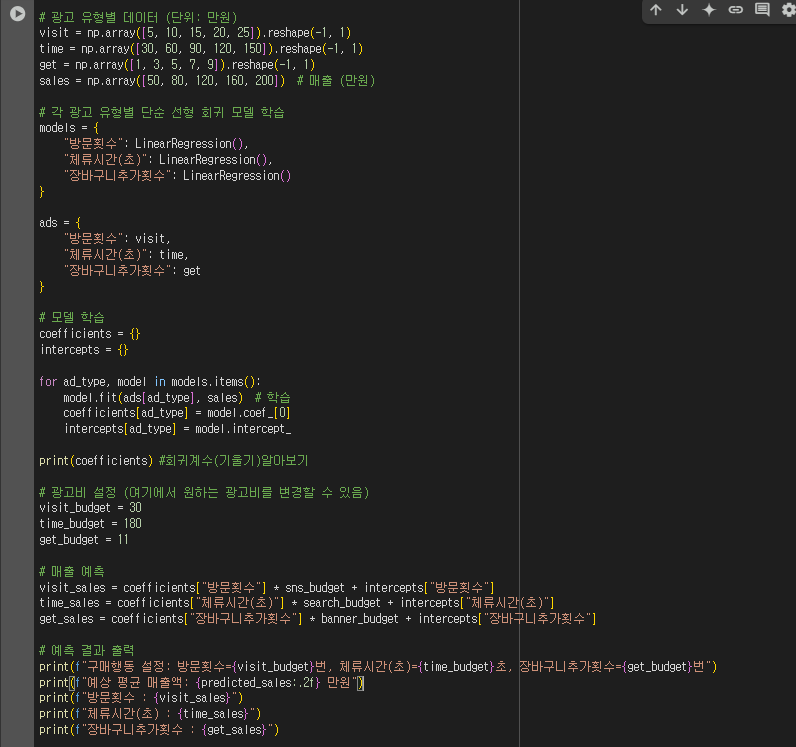
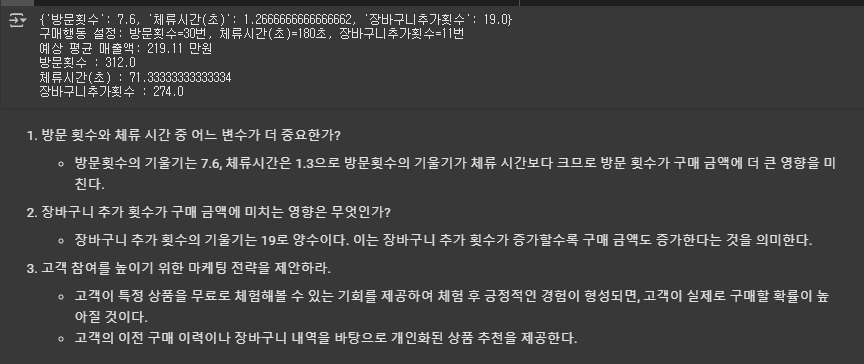
3-2) 웹사이트 방문과 구매 금액 관계 분석
- 한 이커머스 사이트에서 고객의 행동이 구매 금액에 미치는 영향을 분석하고자 한다.
| 방문 횟수 | 체류 시간(초) | 장바구니 추가 횟수 | 구매 금액(만원) |
| 5 | 30 | 1 | 50 |
| 10 | 60 | 3 | 80 |
| 15 | 90 | 5 | 120 |
| 20 | 120 | 7 | 160 |
| 25 | 150 | 9 | 200 |
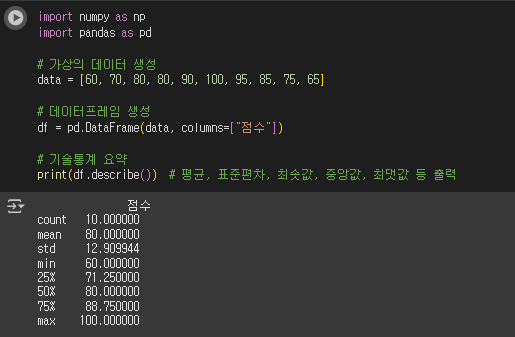
4) 기술통계(Descriptive Statistics) 예제
(4-1) 데이터 생성 및 요약
import numpy as np
import pandas as pd
# 가상의 데이터 생성
data = [60, 70, 80, 80, 90, 100, 95, 85, 75, 65]
# 데이터프레임 생성
df = pd.DataFrame(data, columns=["점수"])
# 기술통계 요약
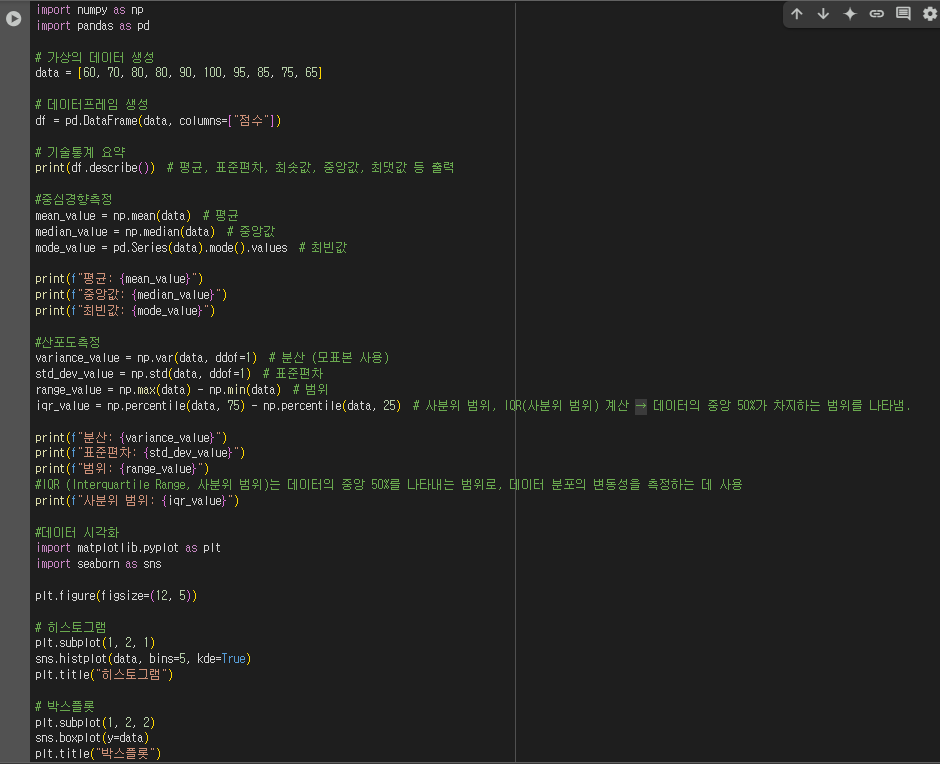
print(df.describe()) # 평균, 표준편차, 최솟값, 중앙값, 최댓값 등 출력
(4-2) 중심 경향 측정
mean_value = np.mean(data) # 평균
median_value = np.median(data) # 중앙값
mode_value = pd.Series(data).mode().values # 최빈값
print(f"평균: {mean_value}")
print(f"중앙값: {median_value}")
print(f"최빈값: {mode_value}")
(4-3) 산포도 측정
variance_value = np.var(data, ddof=1) # 분산 (모표본 사용)
std_dev_value = np.std(data, ddof=1) # 표준편차
range_value = np.max(data) - np.min(data) # 범위
iqr_value = np.percentile(data, 75) - np.percentile(data, 25) # 사분위 범위, IQR(사분위 범위) 계산 → 데이터의 중앙 50%가 차지하는 범위를 나타냄.
print(f"분산: {variance_value}")
print(f"표준편차: {std_dev_value}")
print(f"범위: {range_value}")
#IQR (Interquartile Range, 사분위 범위)는 데이터의 중앙 50%를 나타내는 범위로, 데이터 분포의 변동성을 측정하는 데 사용
print(f"사분위 범위: {iqr_value}")
(4-4) 데이터 시각화
import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(12, 5))
# 히스토그램
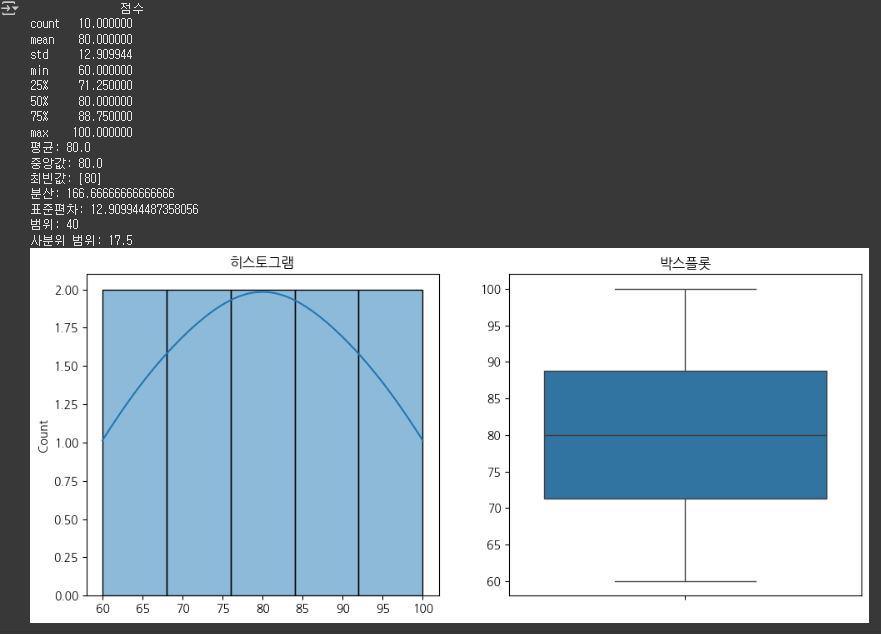
plt.subplot(1, 2, 1)
sns.histplot(data, bins=5, kde=True)
plt.title("히스토그램")
# 박스플롯
plt.subplot(1, 2, 2)
sns.boxplot(y=data)
plt.title("박스플롯")
plt.show()
3. 데이터 분포와 확률의 관계
- 확률 분포(Probability Distribution)는 특정 확률을 기반으로 데이터가 어떻게 분포하는지를 설명
- 정규 분포, 이항 분포, 포아송 분포 등은 각각의 확률 법칙을 따름
- 통계적 추론(Statistical Inference)을 통해 데이터에서 확률을 추정하고, 이를 바탕으로 미래를 예측
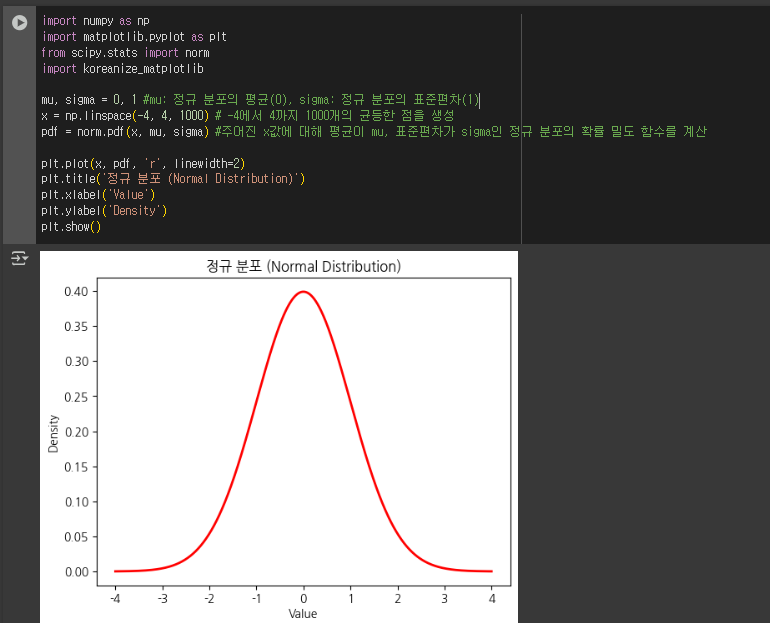
1) 정규 분포 (Normal Distribution)
- 종 모양(Bell Curve)을 가진 대칭적인 분포
- 평균(μ)과 표준편차(σ)로 정의됨
- 자연현상과 많은 데이터셋에서 흔히 나타남
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
mu, sigma = 0, 1
x = np.linspace(-4, 4, 1000)
pdf = norm.pdf(x, mu, sigma)
plt.plot(x, pdf, 'r', linewidth=2)
plt.title('정규 분포 (Normal Distribution)')
plt.xlabel('Value')
plt.ylabel('Density')
plt.show()
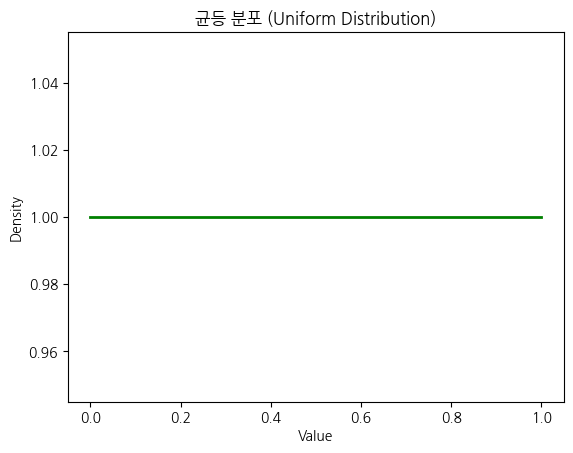
2) 균등 분포 (Uniform Distribution)
- 모든 값이 동일한 확률을 가짐
- 예: 주사위를 던질 때 각 면이 나올 확률이 동일함
from scipy.stats import uniform
x = np.linspace(0, 1, 1000)
pdf = uniform.pdf(x, 0, 1)
plt.plot(x, pdf, 'g', linewidth=2)
plt.title('균등 분포 (Uniform Distribution)')
plt.xlabel('Value')
plt.ylabel('Density')
plt.show()
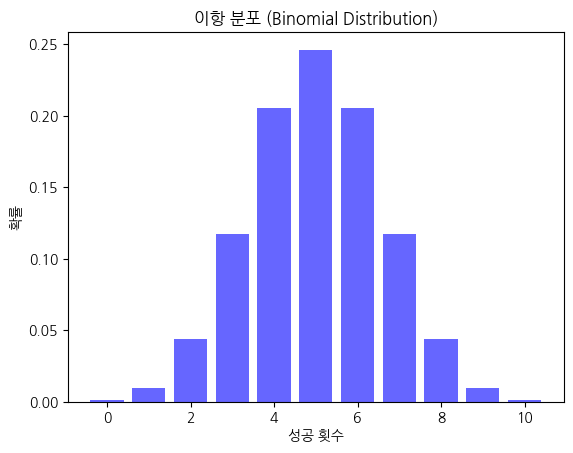
3) 이항 분포 (Binomial Distribution)
- 특정 사건이 여러 번 반복될 때, 성공과 실패의 횟수를 따지는 분포
- 예: 동전을 10번 던졌을 때 앞면이 나오는 횟수
from scipy.stats import binom
n, p = 10, 0.5
x = np.arange(0, n+1)
pmf = binom.pmf(x, n, p)
plt.bar(x, pmf, color='blue', alpha=0.6)
plt.title('이항 분포 (Binomial Distribution)')
plt.xlabel('성공 횟수')
plt.ylabel('확률')
plt.show()
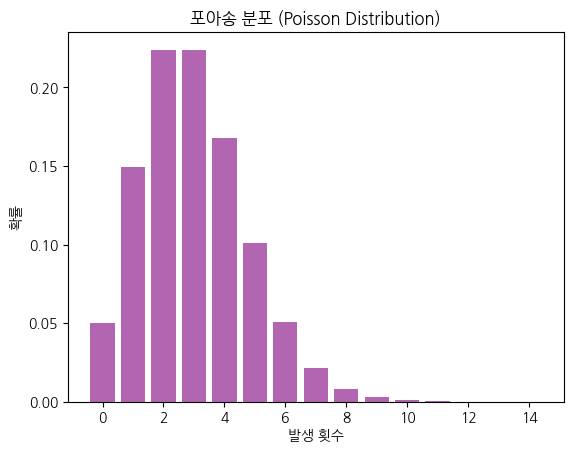
4) 포아송 분포 (Poisson Distribution)
- 일정 시간이나 공간 내에서 발생하는 사건의 횟수를 모델링
- 예: 고객이 1시간 동안 매장에 방문하는 횟수
from scipy.stats import poisson
lambda_ = 3
x = np.arange(0, 15)
pmf = poisson.pmf(x, lambda_)
plt.bar(x, pmf, color='purple', alpha=0.6)
plt.title('포아송 분포 (Poisson Distribution)')
plt.xlabel('발생 횟수')
plt.ylabel('확률')
plt.show()
회귀분석, 단순 회귀 및 다중 회귀
1. 단순회귀분석의 개념과 단순 회귀
- 회귀분석은 통계학에서 두 개 이상의 변수 사이의 관계를 분석하고 예측 모델을 구축하는 기법
- 변수 간의 상관관계를 파악하고, 미래의 값을 예측하거나 변수들이 어떻게 상호작용하는지 이해
1) 주요 구성요소
- 종속 변수 (Dependent Variable, Y): 분석의 목표가 되는 변수. 설명하고자 하는 대상.
- 독립 변수 (Independent Variable, X): 종속 변수에 영향을 주는 변수.
- 오차항 (Error Term, ε): 모델이 설명하지 못하는 부분, 즉 관측된 값과 예측된 값 사이의 차이를 의미.
2) 단순 회귀 분석
- 하나의 독립 변수와 하나의 종속 변수 사이의 선형 관계를 모델링하는 가장 기본적인 형태의 회귀분석.
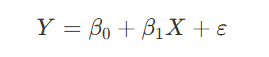
- beta_0 (절편, Intercept): 독립 변수 X의 값이 0일 때 예상되는 종속 변수 Y의 값
- beta_1 (기울기, Slope): X가 한 단위 증가할 때 Y가 평균적으로 얼마나 증가(또는 감소)하는지를 나타낸다.
- $\varepsilon$ (오차항): 모델이 설명하지 못한 변동성.
3) 회귀분석의 기본 가정
- 선형성 (Linearity): 독립 변수와 종속 변수 간의 관계가 선형이라는 가정. 데이터가 선형적이지 않을 경우 비선형 변환이나 다른 모델링 기법이 필요할 수 있다.
- 독립성 (Independence): 각 관측치가 서로 독립적이어야 한다. 시간 순서가 있는 데이터의 경우 자기상관 문제가 발생할 수 있으며, 이를 확인하고 보정할 필요가 있다.
- 등분산성 (Homoscedasticity): 모든 수준의 독립 변수에서 오차의 분산이 동일하다는 가정. 만약 오차의 분산이 일정하지 않다면(이분산성), 모델의 추정치가 왜곡될 수 있다.
- 정규성 (Normality): 오차항이 정규분포를 따른다는 가정, 정규성 검정을 통해 확인할 수 있다.
5) 모델 적합도 평가 및 검정.
- 결정계수 (R²)
- R² 값: 종속 변수의 변동 중에서 모델이 설명하는 비율. 0과 1 사이의 값을 가진다
- R² 값이 1에 가까울수록 모델이 데이터를 잘 설명함을 의미.
- R² = 0이면 모델이 평균값만큼도 설명하지 못한다는 뜻.
- R² 가 음수일 수도 있으며, 이는 모델이 데이터 설명에 실패하고 있음(즉, 평균값을 그대로 예측하는 것보다 성능이 나쁨)을 의미.
- 추가적으로, 다중 회귀에서는 조정 결정계수를 사용하는 것이 더 적절할 수도 있다.
- R² 값: 종속 변수의 변동 중에서 모델이 설명하는 비율. 0과 1 사이의 값을 가진다
- t-검정 및 p-값
- t-검정: 각 회귀계수가 통계적으로 유의한지를 검정.
- p-값: 기울기나 절편이 0이라는 귀무가설을 기각할 수 있는지 판단. 일반적으로 p-값이 0.05 미만이면 유의.
- F-검정
- 전체 모델의 유의성을 검정하는 방법으로, 독립 변수가 종속 변수의 변동을 설명하는 데 유의한지를 평가.
6) 회귀분석의 한계와 주의점
- 상관관계와 인과관계: 회귀분석은 변수 간 상관관계를 분석하지만, 인과관계를 확정하지는 않는다.
- 가정 위배: 선형성, 독립성, 등분산성, 정규성 등의 가정이 위배되면 모델의 추정치와 해석에 문제가 발생할 수 있다.
- 외생 변수: 중요한 독립 변수가 누락되면, 결과가 왜곡될 수 있다.
- 이상치의 영향: 이상치는 회귀계수 추정에 큰 영향을 미칠 수 있으므로, 데이터 전처리와 이상치 처리가 필요하다.
2. 단순회귀분석에 대한 그로스 마케팅 시나리오
1) 시나리오 1
- 목표: 광고비를 최적화하여 전환수를 극대화하고, 효율적인 마케팅 전략을 수립합니다.
- 방법:
- 과거 일정 기간 동안 광고비와 전환수 데이터를 수집합니다.
- 단순 회귀 분석을 통해 광고비(독립 변수)와 전환수(종속 변수) 간의 선형 관계를 모델링합니다.
- 모델을 통해 광고비가 1단위 증가할 때 예상되는 전환수의 변화(기울기)와, 광고비 0일 때의 예상 전환수(절편)를 파악합니다.
- 결정계수(R²)를 이용해 모델의 설명력을 평가하고, 마케팅 전략의 효과를 검증합니다.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
# 1. 가상의 데이터 생성
np.random.seed(42) # 결과 재현을 위한 시드 설정
# 광고비 데이터: 1,000 ~ 10,000 달러 사이의 50개 포인트
ad_spend = np.linspace(1000, 10000, 50)
# 실제 전환수: 실제로는 광고비가 증가할수록 전환수가 증가한다고 가정
# 실제 모형: conversions = intercept + slope * ad_spend + noise
true_intercept = 50 # 광고비 0일 때 기본 전환수
true_slope = 0.05 # 광고비 1달러 증가당 전환수 증가량
noise = np.random.normal(0, 30, ad_spend.shape[0]) # 랜덤 노이즈 추가
conversions = true_intercept + true_slope * ad_spend + noise
# 데이터프레임 생성
df = pd.DataFrame({'ad_spend': ad_spend, 'conversions': conversions})
# 2. 회귀분석을 위한 데이터 준비
X = df[['ad_spend']] # 독립 변수 (광고비)
y = df['conversions'] # 종속 변수 (전환수)
# 3. 단순 회귀 모델 생성 및 학습
model = LinearRegression()
model.fit(X, y)
# 4. 모델 파라미터 출력
print("모델 절편 (Intercept):", model.intercept_)
print("모델 기울기 (Slope):", model.coef_[0])
# 5. 예측값 계산 및 결정계수 평가
y_pred = model.predict(X)
print("결정계수 (R²):", r2_score(y, y_pred))
# 6. 결과 시각화
plt.scatter(df['ad_spend'], df['conversions'], color='blue', label='실제 데이터')
plt.plot(df['ad_spend'], y_pred, color='red', label='회귀 직선')
plt.title('광고비 대비 전환수 분석')
plt.xlabel('광고비 ($)')
plt.ylabel('전환수')
plt.legend()
plt.show()

2) 시나리오2
- 한 온라인 쇼핑몰의 마케팅 팀은 광고비(달러)와 전환수(신규 고객 획득 또는 구매 건수) 간의 관계를 분석하여, 광고비 지출의 효율성을 평가하고 향후 예산 배분 전략을 수립하려고 합니다. 이를 위해 단순 회귀 분석을 수행하여 광고비가 전환수에 미치는 영향을 파악합니다.
- 가상의 데이터 표
| 광고비 (달러) | 전환수 |
| 1,000 | 105 |
| 3,000 | 195 |
| 5,000 | 310 |
| 7,000 | 395 |
| 9,000 | 505 |
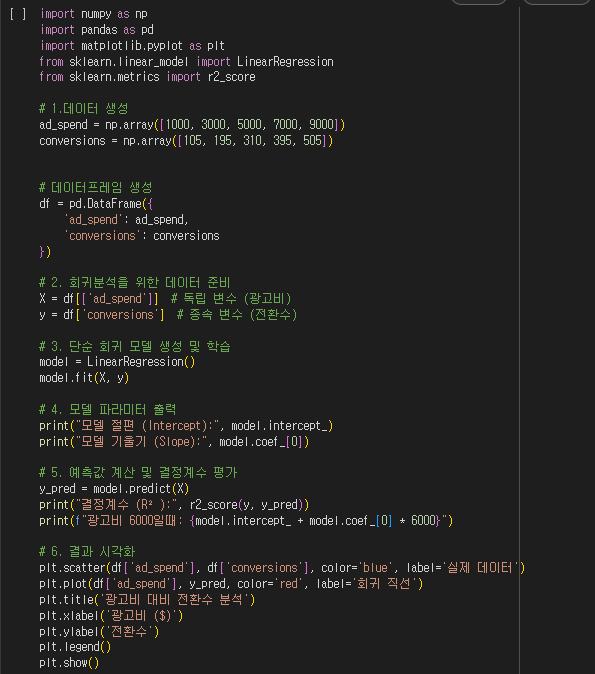
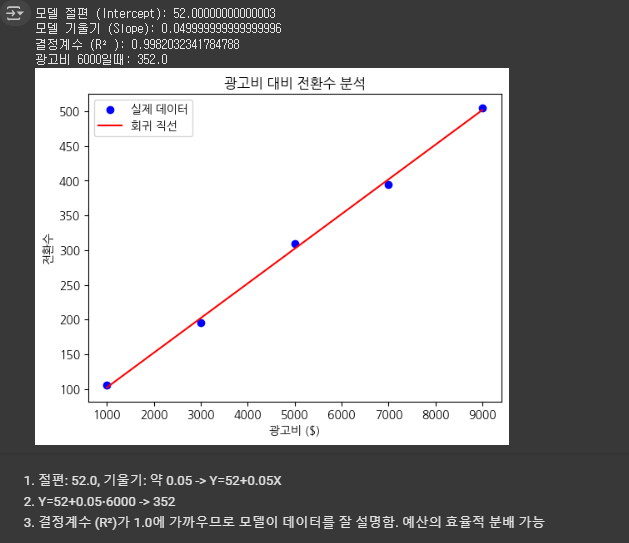
문제 1. 단순 회귀 분석 수행
- 기울기를 추정하고, 회귀식을 도출하세요.
문제 2. 예측 및 해석
- 학광고비가 6,000달러일 때 예상되는 전환수를 예측 하시오. 예측 결과에 대한 해석도 함께 기술하세요.
문제 3. 모델 적합도 평가
- 결정계수가 의미하는 바와, 마케팅 전략 수립 시 어떻게 활용할 수 있는지 서술하세요.
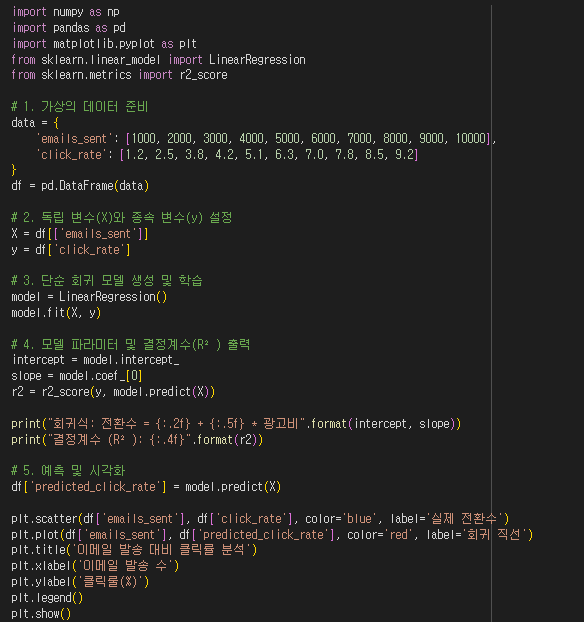
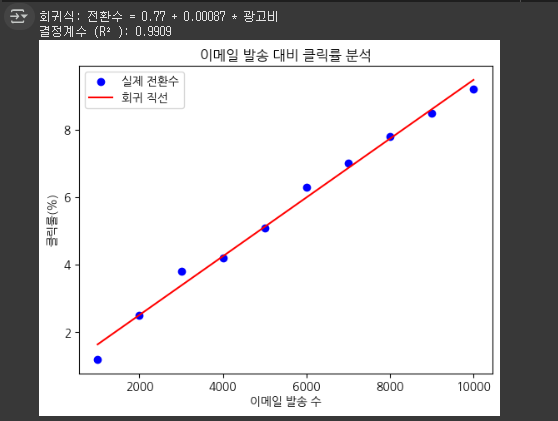
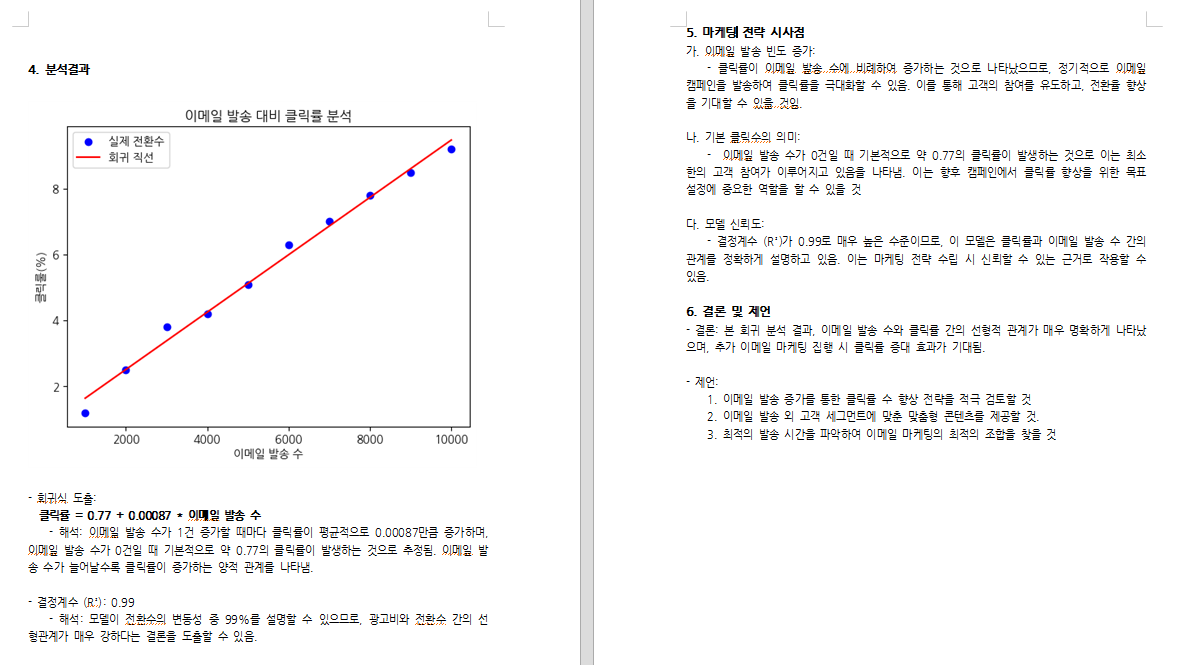
3) 회귀분석 기반 보고서 연습 (주제 : 이메일 마케팅 캠페인 발송 수에 따른 클릭률)
- 다음의 표에서 제시한 데이터를 이용해 회귀식을 만들고 위 예에서 제시한 보고서 형식을 사용해 마케팅 보고서를 작성하세요.
| 발송한 이메일 수 (emails_sent) | 클릭률 (%) (click_rate |
| 1000 | 1.2 |
| 2000 | 2.5 |
| 3000 | 3.8 |
| 4000 | 4.2 |
| 5000 | 5.1 |
| 6000 | 6.3 |
| 7000 | 7.0 |
| 8000 | 7.8 |
| 9000 | 8.5 |
| 10000 | 9.2 |
3. 다중 회귀 분석의 기본 개념
- 단순 회귀 분석의 확장으로, 하나의 종속 변수와 두 개 이상의 독립 변수 간의 관계를 동시에 분석하는 통계적 기법.
- 이를 통해 여러 요인이 종속 변수에 미치는 영향을 동시에 고려할 수 있으며, 보다 정교한 예측 모델을 구축
1) 모델 수식
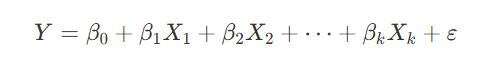
- Y: 종속 변수 (예측하려는 값)
- X_1, X_2 ~: 여러 독립 변수들
- beta_0: 절편 (모든 독립 변수의 값이 0일 때의 예상 값)
- beta_1, beta_2 ~: 각 독립 변수의 회귀 계수로, 다른 변수들이 고정된 상태에서 해당 독립 변수가 에 미치는 영향을 나타낸다.
- $\varepsilon$: 오차항으로, 모델이 설명하지 못하는 변동성을 포함.
2) 모델 평가
- 결정계수 ( R² ): 모델이 종속 변수의 변동성을 얼마나 설명하는지를 나타내며, 0과 1 사이의 값을 가진다.
- 조정된 결정계수 (Adjusted R² ): 독립 변수의 개수가 늘어날 때 발생할 수 있는 과적합 문제를 보정하기 위해 사용
- F-검정: 전체 모델의 유의성을 평가하여, 적어도 하나의 독립 변수가 종속 변수와 유의한 관계가 있는지를 검정.
3) 다중 회귀 분석의 장점 및 한계
- 장점
- 복합 요인 분석: 여러 독립 변수가 동시에 종속 변수에 미치는 영향을 고려할 수 있으므로, 보다 현실적인 모델링이 가능.
- 예측력 향상: 여러 변수들을 포함함으로써 단순 회귀 분석보다 설명력이 높은 모델을 구축할 수 있다.
- 한계
- 모형 복잡성: 독립 변수의 수가 많아질수록 모델의 복잡성이 증가하고, 과적합(overfitting) 위험이 커질 수 있다.
- 다중공선성 문제: 독립 변수들 간의 상관관계가 높으면 계수 추정이 불안정해지고 해석이 어려워질 수 있다.
- 가정 위배: 기본 가정(선형성, 독립성, 등분산성, 정규성)이 위배될 경우, 모델의 신뢰도가 떨어지게 된다.
4. 다중회귀분석에 대한 그로스 마케팅 시나리오
1) 예시 코드
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
# 가상의 데이터 생성
# 예: 매출(Y)은 광고비(X1)와 프로모션 예산(X2)의 영향을 받음
np.random.seed(42)
n = 50
ad_spend = np.random.uniform(1000, 10000, n) # 광고비 (달러)
promo_budget = np.random.uniform(500, 5000, n) # 프로모션 예산 (달러)
# 실제 모델: Y = 50 + 0.03*ad_spend + 0.05*promo_budget + noise
true_intercept = 50
true_coef_ad = 0.03
true_coef_promo = 0.05
noise = np.random.normal(0, 30, n)
sales = true_intercept + true_coef_ad * ad_spend + true_coef_promo * promo_budget + noise
# 데이터프레임 생성
df = pd.DataFrame({
'ad_spend': ad_spend,
'promo_budget': promo_budget,
'sales': sales
})
# 독립 변수와 종속 변수 설정
X = df[['ad_spend', 'promo_budget']]
y = df['sales']
# 다중 회귀 모델 생성 및 학습
model = LinearRegression()
model.fit(X, y)
# 모델 파라미터 및 결정계수 출력
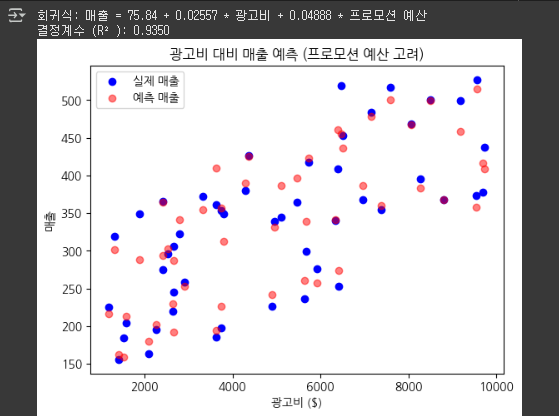
print("회귀식: 매출 = {:.2f} + {:.5f} * 광고비 + {:.5f} * 프로모션 예산".format(
model.intercept_, model.coef_[0], model.coef_[1]
))
print("결정계수 (R²): {:.4f}".format(r2_score(y, model.predict(X))))
# 산점도와 회귀면 시각화(2차원 시각화는 독립 변수가 2개이므로 다소 복잡할 수 있음)
# 여기서는 광고비에 따른 예측 매출을 예시로 시각화합니다.
plt.scatter(df['ad_spend'], y, color='blue', label='실제 매출')
plt.scatter(df['ad_spend'], model.predict(X), color='red', label='예측 매출', alpha=0.5)
plt.xlabel('광고비 ($)')
plt.ylabel('매출')
plt.title('광고비 대비 매출 예측 (프로모션 예산 고려)')
plt.legend()
plt.show()
2) 시나리오 1
- 목표: 온라인 쇼핑몰에서 매출 증대를 위해 다음과 같은 여러 요인이 매출에 미치는 영향을 파악하고자 합니다.
- 분석 대상 변수:
- 광고비 (ad_spend): 온라인 광고 집행에 사용한 예산 (달러)
- 프로모션 예산 (promo_budget): 할인, 쿠폰, 이벤트 등 프로모션에 투자한 예산 (달러)
- 웹사이트 방문자 수 (website_traffic): 캠페인 기간 동안 유입된 방문자 수 (명)
- 매출 (sales): 각 캠페인에서 발생한 총 매출 (달러)
- 분석 목적:
- 다중 회귀 분석을 통해 각 마케팅 활동이 매출에 미치는 영향을 정량화하고,
- 어떤 요인이 매출 증대에 가장 크게 기여하는지 파악
- 미래 캠페인 및 예산 배분 전략을 최적화
| 광고비 (달러) | 프로모션 예산 (달러) | 웹사이트 방문자 수 (명) | 매출 (달러) |
| 1,000 | 500 | 2,000 | 15,000 |
| 2,000 | 700 | 2,500 | 18,000 |
| 3,000 | 900 | 3,000 | 22,000 |
| 4,000 | 1,100 | 3,500 | 25,000 |
| 5,000 | 1,300 | 4,000 | 29,000 |
| 6,000 | 1,500 | 4,500 | 32,000 |
| 7,000 | 1,700 | 5,000 | 36,000 |
| 8,000 | 1,900 | 5,500 | 40,000 |
| 9,000 | 2,100 | 6,000 | 44,000 |
| 10,000 | 2,300 | 6,500 | 48,000 |
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
# 1. 가상의 데이터 준비
data = {
'ad_spend': [1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000, 9000, 10000],
'promo_budget': [500, 700, 900, 1100, 1300, 1500, 1700, 1900, 2100, 2300],
'website_traffic': [2000, 2500, 3000, 3500, 4000, 4500, 5000, 5500, 6000, 6500],
'sales': [15000, 18000, 22000, 25000, 29000, 32000, 36000, 40000, 44000, 48000]
}
df = pd.DataFrame(data)
# 2. 독립 변수와 종속 변수 설정
X = df[['ad_spend', 'promo_budget', 'website_traffic']]
y = df['sales']
# 3. 다중 회귀 모델 생성 및 학습
model = LinearRegression()
model.fit(X, y)
# 4. 모델 파라미터 및 결정계수(R²) 출력
print("회귀식: 매출 = {:.2f} + {:.5f} * 광고비 + {:.5f} * 프로모션 예산 + {:.5f} * 웹사이트 방문자 수".format(
model.intercept_, model.coef_[0], model.coef_[1], model.coef_[2]
))
print("결정계수 (R²): {:.4f}".format(r2_score(y, model.predict(X))))
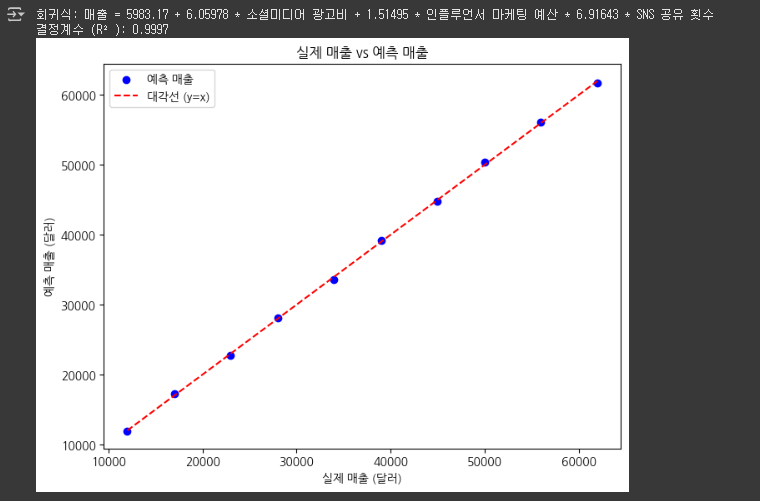
# 5. 예측 결과: 실제 매출과 예측 매출 비교
predicted_sales = model.predict(X)
plt.figure(figsize=(8, 6))
plt.scatter(y, predicted_sales, color='blue', label='예측 매출')
plt.plot([min(y), max(y)], [min(y), max(y)], color='red', linestyle='--', label='대각선 (y=x)')
plt.xlabel('실제 매출 (달러)')
plt.ylabel('예측 매출 (달러)')
plt.title('실제 매출 vs 예측 매출')
plt.legend()
plt.show()
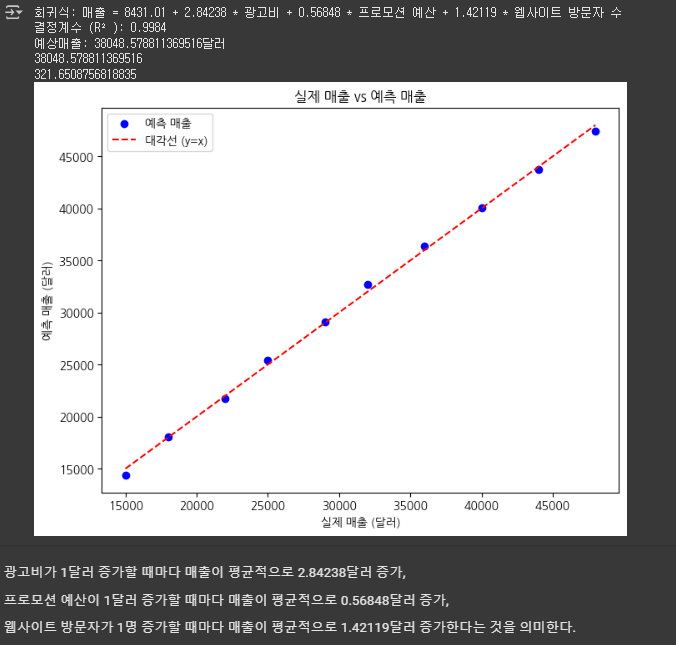
3) 다중회귀분석 기반 보고서 연습 1
- 개요
- 본 보고서는 온라인 쇼핑몰에서 진행한 10개 캠페인의 데이터를 바탕으로, 광고비, 프로모션 예산, 웹사이트 방문자 수가 매출에 미치는 복합적 영향을 분석하였습니다. 이를 통해 각 마케팅 활동의 기여도를 파악하고, 효율적인 예산 배분 및 향후 캠페인 전략 수립을 위한 인사이트를 도출하는 데 목적이 있습니다.
- 데이터 및 분석 방법
- 데이터: 10개 캠페인에서 집계한 광고비, 프로모션 예산, 웹사이트 방문자 수, 그리고 매출 데이터
- 분석 방법:
- 다중 회귀 분석을 활용하여, 광고비, 프로모션 예산, 웹사이트 방문자 수가 매출에 미치는 영향을 동시에 평가
- 모델의 결정계수(R²)를 통해 설명력을 검증
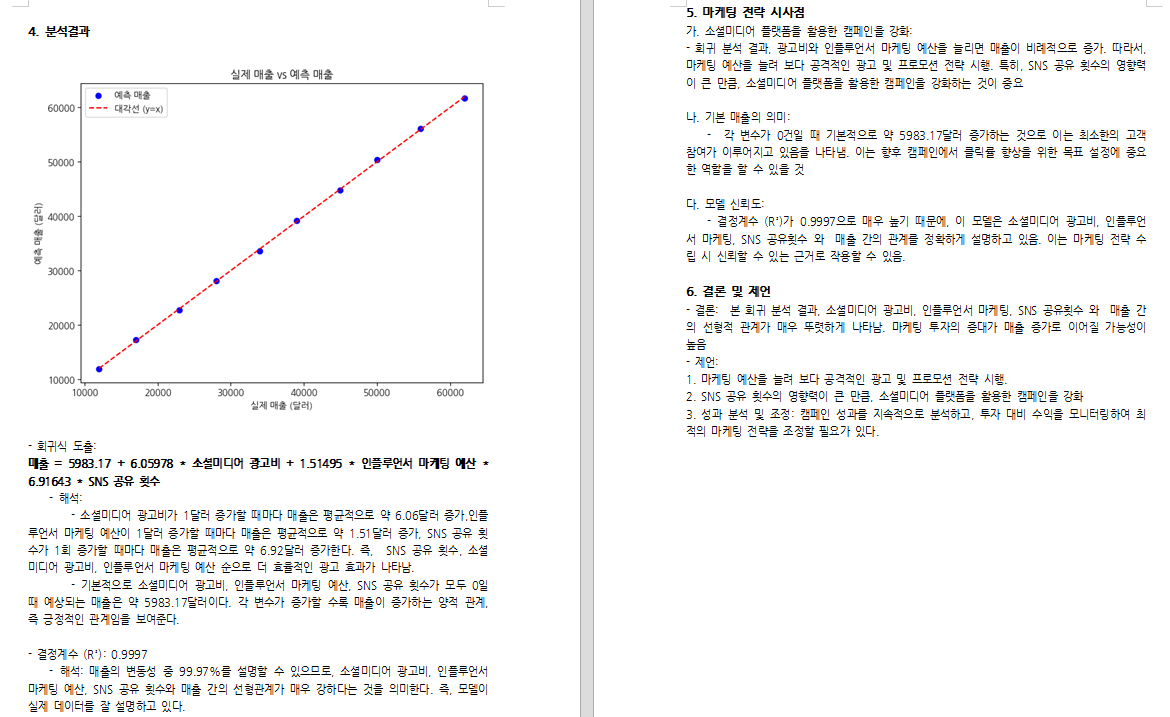
5. 다중 회귀 분석을 통해 얻을 수 있는 주요 인사이트
- 그로스 마케팅에서 다중 회귀 분석은 필수적인 도구이며, 마케팅 성과를 최적화하고 ROI를 극대화하는 데 활용할 수 있다.
- 광고비, 웹사이트 방문자 수, 구매 전환율, 할인율, 고객 유지율 등 다양한 요소들이 매출에 미치는 영향을 분석하여 데이터 기반 의사결정을 가능하게 한다.
- 단순히 광고비를 늘리는 것보다 효과적인 전략(예: 전환율 최적화, 리텐션 강화)을 선택하는 것이 더욱 중요할 수 있다.
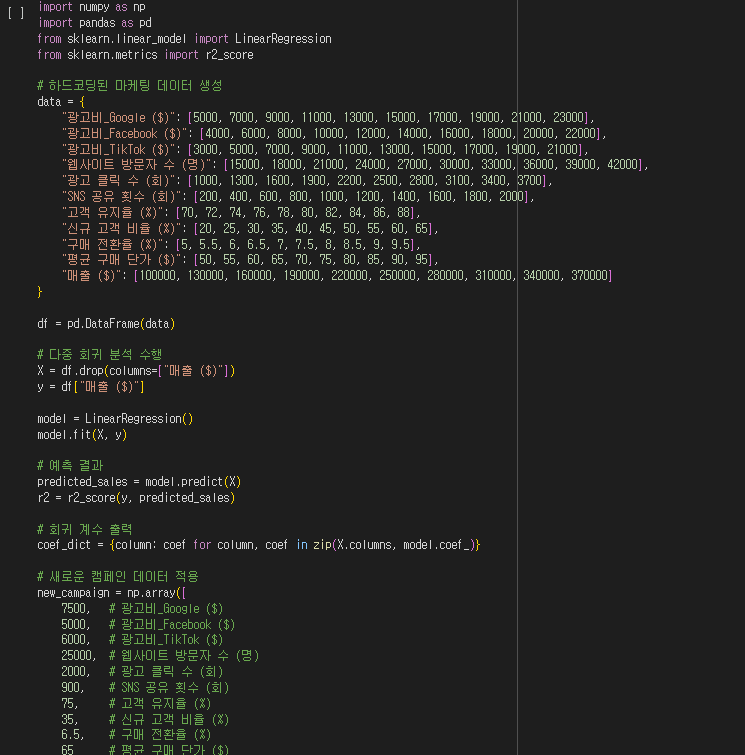
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
# 하드코딩된 마케팅 데이터 생성
data = {
"광고비_Google ($)": [5000, 7000, 9000, 11000, 13000, 15000, 17000, 19000, 21000, 23000],
"광고비_Facebook ($)": [4000, 6000, 8000, 10000, 12000, 14000, 16000, 18000, 20000, 22000],
"광고비_TikTok ($)": [3000, 5000, 7000, 9000, 11000, 13000, 15000, 17000, 19000, 21000],
"웹사이트 방문자 수 (명)": [15000, 18000, 21000, 24000, 27000, 30000, 33000, 36000, 39000, 42000],
"광고 클릭 수 (회)": [1000, 1300, 1600, 1900, 2200, 2500, 2800, 3100, 3400, 3700],
"SNS 공유 횟수 (회)": [200, 400, 600, 800, 1000, 1200, 1400, 1600, 1800, 2000],
"고객 유지율 (%)": [70, 72, 74, 76, 78, 80, 82, 84, 86, 88],
"신규 고객 비율 (%)": [20, 25, 30, 35, 40, 45, 50, 55, 60, 65],
"구매 전환율 (%)": [5, 5.5, 6, 6.5, 7, 7.5, 8, 8.5, 9, 9.5],
"평균 구매 단가 ($)": [50, 55, 60, 65, 70, 75, 80, 85, 90, 95],
"매출 ($)": [100000, 130000, 160000, 190000, 220000, 250000, 280000, 310000, 340000, 370000]
}
df = pd.DataFrame(data)
# 다중 회귀 분석 수행
X = df.drop(columns=["매출 ($)"])
y = df["매출 ($)"]
model = LinearRegression()
model.fit(X, y)
# 예측 결과
predicted_sales = model.predict(X)
r2 = r2_score(y, predicted_sales)
# 회귀 계수 출력
coef_dict = {column: coef for column, coef in zip(X.columns, model.coef_)}
# 새로운 캠페인 데이터 적용
new_campaign = np.array([
7500, # 광고비_Google ($)
5000, # 광고비_Facebook ($)
6000, # 광고비_TikTok ($)
25000, # 웹사이트 방문자 수 (명)
2000, # 광고 클릭 수 (회)
900, # SNS 공유 횟수 (회)
75, # 고객 유지율 (%)
35, # 신규 고객 비율 (%)
6.5, # 구매 전환율 (%)
65 # 평균 구매 단가 ($)
]).reshape(1, -1)
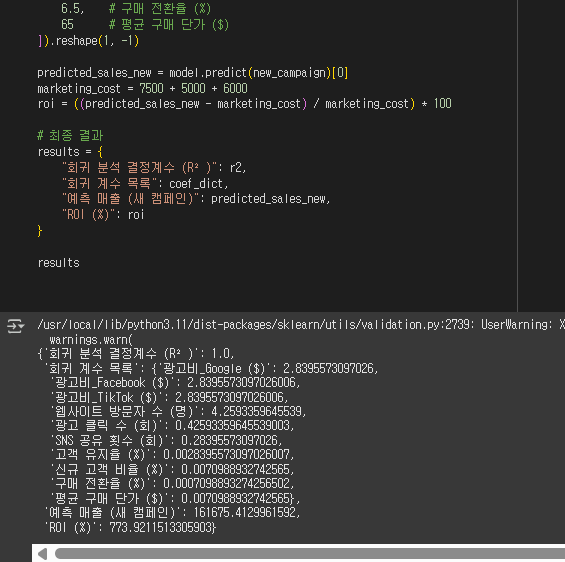
predicted_sales_new = model.predict(new_campaign)[0]
marketing_cost = 7500 + 5000 + 6000
roi = ((predicted_sales_new - marketing_cost) / marketing_cost) * 100
# 최종 결과
results = {
"회귀 분석 결정계수 (R²)": r2,
"회귀 계수 목록": coef_dict,
"예측 매출 (새 캠페인)": predicted_sales_new,
"ROI (%)": roi
}
results
- 문제 1: 다중 회귀 분석 해석
- 가장 높은 영향력을 가지는 변수는 무엇인가?
- 특정 변수(예: SNS 공유 횟수)가 음수의 회귀 계수를 가지면 어떤 의미인가?
- 문제 2: ROI 계산
- 위 데이터를 다중 회귀 모델에 적용하여 새로운 캠페인의 예상 매출을 예측하시오.
- 총 마케팅 비용이 광고비_Google + 광고비_Facebook + 광고비_TikTok이라고 가정할 때, ROI를 계산하시오.